Weisfeiler-Lehman Algorithm

Weisfeiler-Lehman Algorithm

Graph Isomorphism

주어진 두 그래프 \(G = (V_{G},E_{G})\) 와 \(H=(V_{H}, E_{H})\) 에 대해, 두 그래프가 isomorphic 하다는 것은 다음을 만족하는 bijection \(f:V_{G}\rightarrow V_{H}\) 가 존재한다는 뜻입니다.

\[u, v \text{ are adjacent in }G \iff f(u), f(v) \text{ are adjacent in }H\]

즉 \(G\) 에서 edge 로 이웃한 모든 node 들의 쌍에 대해, \(H\) 에서 대응되는 각 node 들의 쌍 또한 edge 로 이웃해 있을 때 isomorphic 하다고 표현합니다.

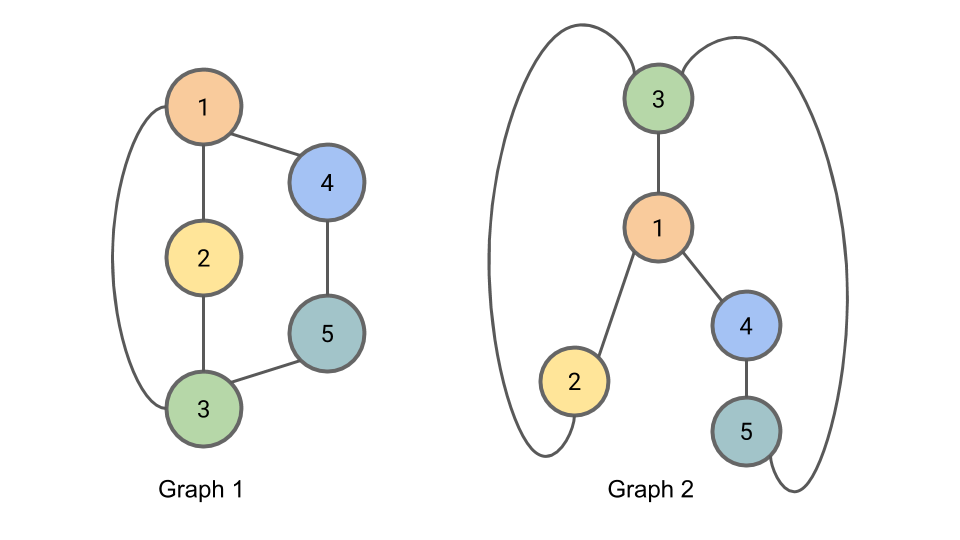
위의 그림에서 보면, 각 그래프에서 같은 숫자를 가진 node 들끼리 대응 되기 때문에, 두 그래프는 isomorphic 합니다.

Weisfeiler-Lehman Algorithm

주어진 두 그래프가 isomorphic 한지를 확인하는 방법으로 Weisfeiler-Lehman algorithm 이 있습니다. 보통 줄여서 WL 알고리즘 혹은 WL test 라고 부릅니다.

1차원의 WL 알고리즘은 다음과 같습니다.

1 차원 WL 알고리즘을 통해 regular graph 를 제외한 대부분의 그래프에 대한 node embedding 이 가능합니다.

주의할 점은 WL 알고리즘의 결과가 다르다면 두 그래프는 확실히 isomorphic 하지 않지만, 결과가 같다고 해서 두 그래프가 isomorphic 하다고는 결론 지을 수 없습니다. Isomorphic 하지 않은 두 그래프의 WL 알고리즘의 결과는 같을 수 있기 때문에, Graph Isomorphism 에 대한 완벽한 해결법이라고는 할 수 없습니다. WL 알고리즘의 반례로는 Reference [3] 을 참고하기 바랍니다.

Example

다음의 두 그래프에 대해 WL 알고리즘을 적용해보겠습니다.

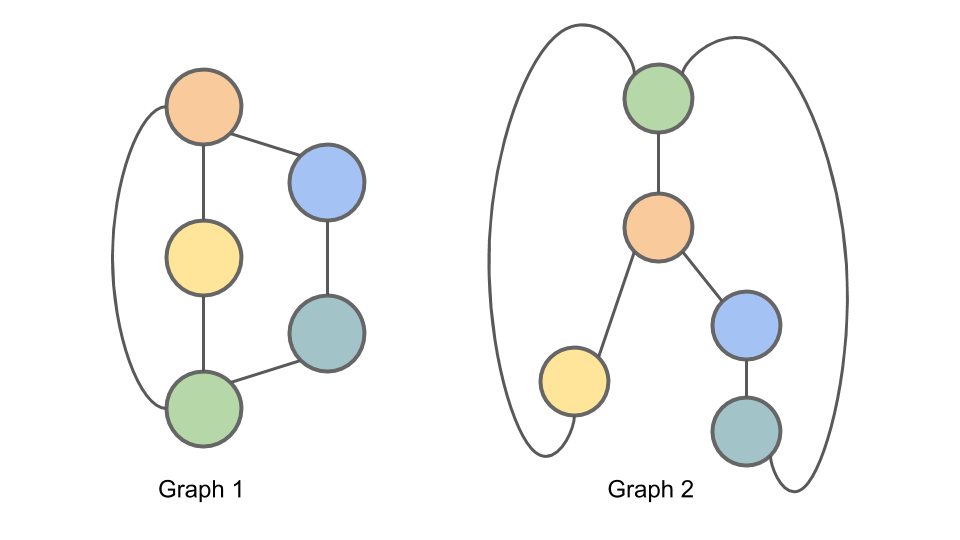
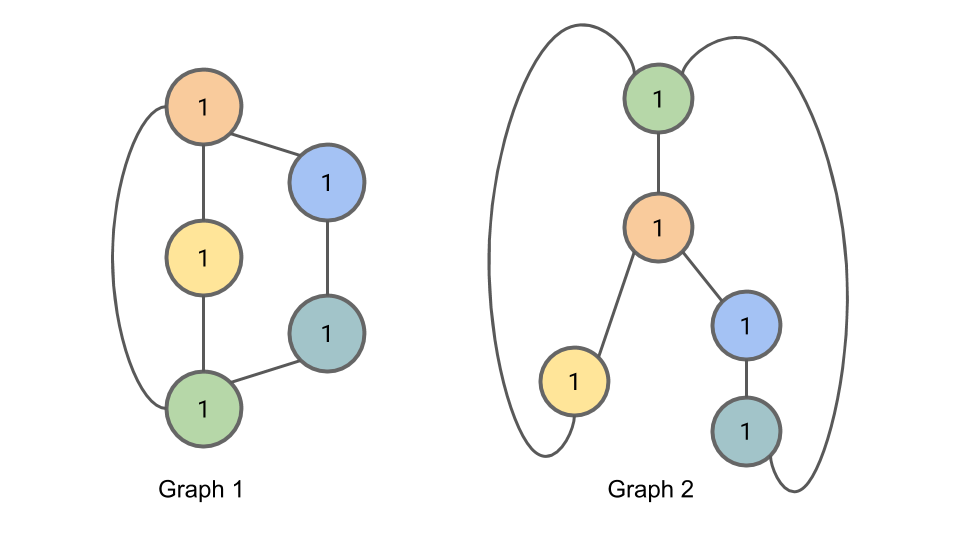
주어진 두 그래프에 대해 initial node coloring \(h^{(0)}_{i}=1\) 을 주겠습니다.

각 node 에 대해 이웃한 node 들의 coloring 정보를 모읍니다. 다음과 같이 multi-set 으로 표시하겠습니다.

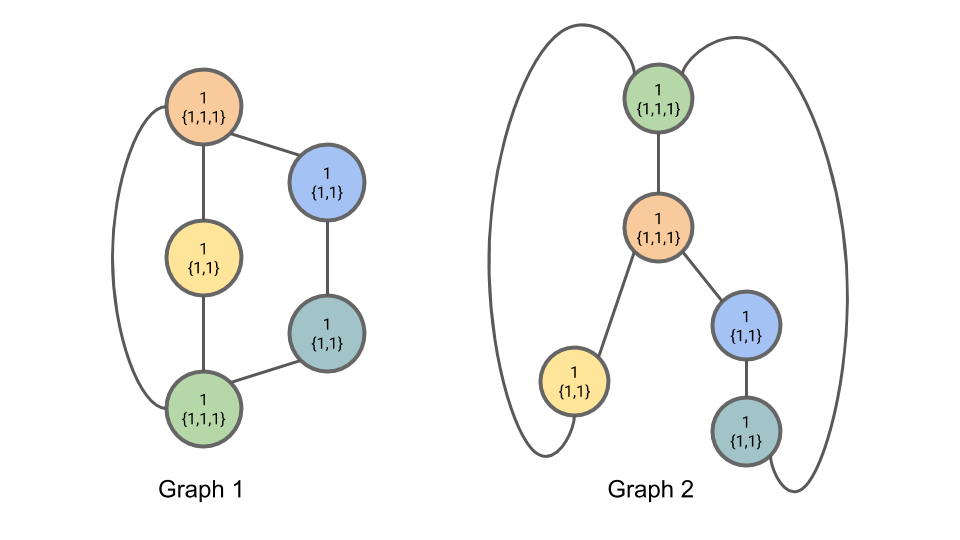
이 예시에서는 편의상 hash 함수로 identity 함수를 사용하겠습니다. 다음과 같이 1 번째 iteration 의 coloring \(h^{(1)}_{i}\) 를 계산할 수 있습니다.

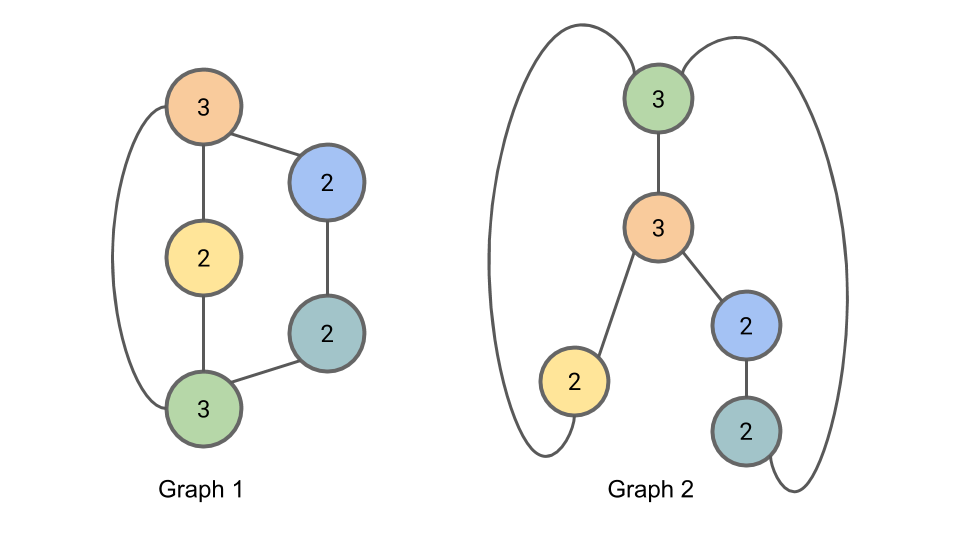
다시 각 node 에 대해 이웃한 node 들의 coloring 정보를 모은 후,

2 번째 iteration 의 coloring \(h^{(2)}_i\) 를 계산해 줍니다.

위의 과정을 반복해 3 번째 iteration 의 coloring \(h^{(3)}_i\) 를 계산해 줍니다.

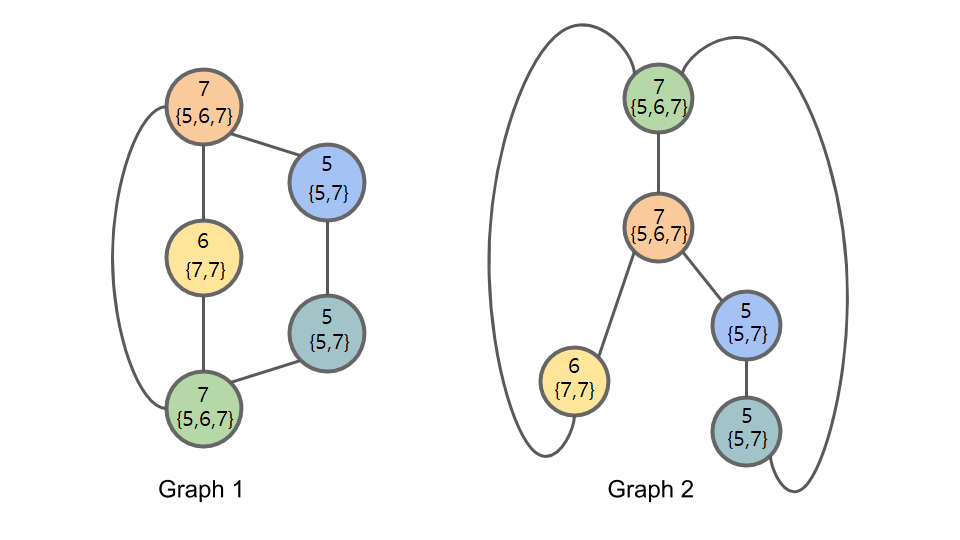
3 번째 iteration 의 coloring 으로 인한 node 들의 분할이 2 번째 iteration 의 분할과 동일하므로, 알고리즘을 끝냅니다. 마지막 그림에서 보다시피, 두 그래프에 대해 WL 알고리즘을 통한 node 들의 분할이 일치합니다. 두 그래프는 실제로 isomorphic 하지만, WL 알고리즘의 결과만으로는 판별할 수 없습니다.

Reference

1. Brendan L. Douglas. The Weisfeiler-Lehman method and graph isomorphism testing. arXiv preprint arXiv:1101.5211, 2011.

2. David Bieber. The Weisfeiler-Lehman Isomorphism Test

3. J. Cai, M. Furer, and N. Immerman. An optimal lower bound on the number of variables for graph identification. Combinatorica, 12(4):389–410, 1992.